What is a Quorum?
In Hemis, a quorum is a subset of randomly selected Gamemaster nodes who each vote to reach consensus on the outcome of a game round played on the Hemis platform.
This article is intended to provide an introduction to the main ways in which Gamemasters and quorums will faciliate game playing on the Hemis blockchain while ensuring that bad actors cannot intefere with games.
Why Quorums?
- Faster Decision Making: Reaching consensus in a large network can be time-consuming, especially if every node has to agree. Using a quorum allows decisions to be made more quickly since only a subset of nodes needs to concur.
- Reduced Network Traffic: Less communication is required to reach a decision among a quorum than the entire network, reducing the bandwidth and computational overhead.
- Handles Network Growth: As the network grows, achieving consensus among all nodes becomes increasingly impractical. A quorum-based approach scales better than standard approaches because it doesn’t require input from every node for each decision.
- Flexible Configuration: Quorum requirements can be adjusted based on the size and needs of the network and the games being played, providing flexibility as the Hemis platform evolves.
How do Quorums work?
The Need for a Decision
Imagine the network needs to confirm a game round, such as Alice and Bob wagering two NFTs on a coin toss. Before it’s accepted as legitimate, this transaction needs a “thumbs up” from a certain number of network participants.
Picking the Jury (Quorum Selection)
Out of all the Gamemasters in the network, a small group is randomly selected to act as a jury. This group is our quorum. Think of it as randomly picking a jury to deliver a verdict on a trial. The goal is to have a fair representation without bias.
The Voting Process
Each member of our jury (the quorum) checks the transaction. They look at details like:
- Do Alice and Bob own the wagered NFTs?
- Is this transaction following all the network rules?
- What are the terms of the wager? Who has heads? Who has tails?
- What was the outcome of the coin toss on the Gamemaster network?
Each Gamemaster in the quorum votes “yes” if everything looks good or “no” if something’s wrong.
Counting the Votes
After all the Gamemasters in the quorum have voted, the votes are tallied. If the majority votes “yes,” the transaction is considered valid and gets a green light. Just like a jury delivering a verdict.
Confirmation and Completion
Once the transaction gets the majority “yes” from the quorum, it’s officially confirmed and added to the blockchain. This is the network’s ledger where all transactions are recorded. Alice won the coin toss and Bob’s NFT is now transferred to Alice, and everyone on the network can see this transaction as valid and confirmed.
Disincentives
By using quorums, we can create significant disincentives to dissuade people from attempting to cheat.
The core of this disincentive lies in the random selection of Gamemasters to form a quorum. This randomness is similar to drawing names from a hat where every Gamemaster in the network has an equal chance of being chosen. To attempt to rig the outcome of a game round by influencing the quorum, a bad actor would need to control a substantial portion of the Gamemaster nodes. This is not just difficult; it’s impractical for several reasons.
Firstly, the financial investment required to acquire control over enough Gamemaster nodes to consistently influence quorum decisions is prohibitively high. Considering the potential cost of acquiring and maintaining these nodes, alongside the uncertain return on such an investment, the economics simply do not add up. The cost of acquiring enough tokens to establish control would likely far exceed any potential gains from influencing a single game round.
Secondly, the logistical challenge of coordinating such an attack compounds its impracticality. Since the selection of Gamemasters for each quorum is random and independent for each game round, an attacker cannot predict which nodes they need to control for any given decision. This unpredictability requires an attacker to maintain control over a significant portion of the network indefinitely, a feat comparable to influencing every possible juror in a judicial system without knowing who will be called to serve.
Maths & Probability of Cheating
How many Gamemaster nodes would a bad actor need to cheat a quorum? For the purposes of this example, let’s assume that there are 1,000 active Gamemasters and a majority vote of a quorum of 11 is required to validate a game round.
The hypergeometric distribution is used for estimating how many Gamemaster nodes are needed to cheat a quorum because it’s ideal for scenarios where selections are made without replacement, which fits the process of selecting Gamemasters for a quorum. The formula for the hypergeometric distribution is:
$$ P(X = k) = \frac{{\binom{K}{k} \cdot \binom{N-K}{n-k}}}{{\binom{N}{n}}} $$
Where:
- N is the total number of Gamemasters (1,000 in our case),
- K is the number of Gamemasters controlled by the attacker,
- n is the size of the quorum (11 here),
- k is the number of controlled Gamemasters in the quorum,
- P(X=k) is the probability that exactly k of the controlled nodes are in the quorum.
For a “reasonable chance” to influence the outcome, let’s interpret this as the attacker controlling the majority of the quorum (i.e., at least 6 out of 11 Gamemasters).
With 5 controlled Gamemasters, the probability of having a majority in the quorum is zero. With 6 controlled nodes we see a probability greater than zero, albeit still extremely low: 10-13 or 1 in 10,000,000,000,000. This represents a one in ten trillion chance.
These probabilities are indicative of how challenging it is to gain a significant influence over the quorum with a small number of Gamemasters under control. To find the point at which the probability becomes non-negligible, you have to perform calculations with much larger numbers of Gamemasters.
Let’s plot these probabilities over the range of controlled Gamemasters to visualise when the chance of influencing the quorum becomes significant.
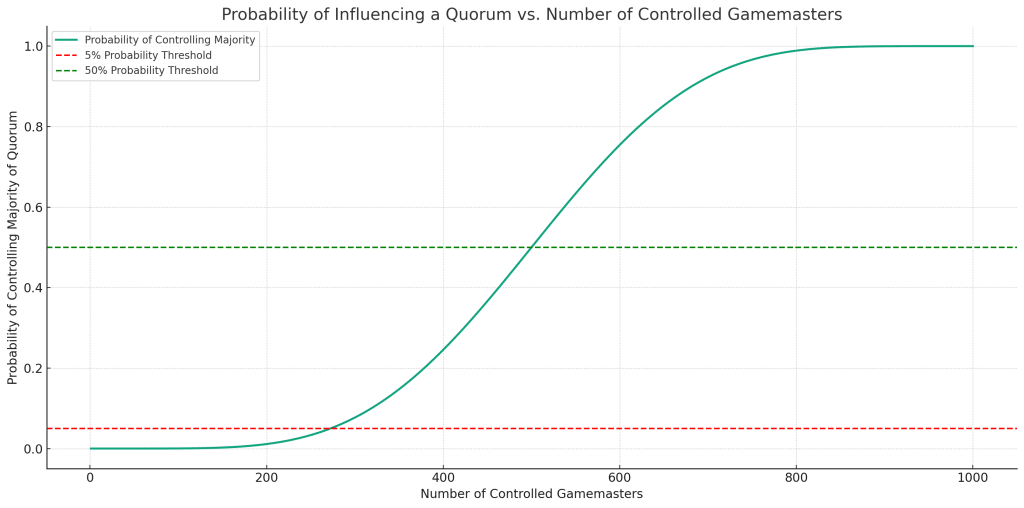
The plot illustrates how the probability of controlling the majority of a quorum increases with the number of Gamemasters controlled by the attacker. It’s evident that as the number of controlled Gamemasters increases the more likely they are to be able to cheat a quorum.
Two key thresholds are marked on the graph:
- A 5% Probability Threshold indicates the point at which there’s a 5% chance of controlling the majority of the quorum. This level might be considered the beginning of a “non-negligible” chance.
- A 50% Probability Threshold represents a tipping point where the attacker is more likely than not to control the majority of the quorum.
The exact point at which these thresholds are crossed will vary based on network parameters and the specific implementation of the Gamemaster algorithm that the Hemis team releases with Probabilistic Transactions in Q1 2025.
IMPORTANT NOTE
All figures used in this article are indicative for explanation purposes and are likely to change as a result of testing before PTX (Probabilistic Transactions) are released in Q1 2025.